SISTEMAS_ELECTRONICOS_PARA_INGENIERIA_BIOMEDICA

Amplificadores

Introducción

En electrónica muchas veces se requiere amplificar señales. En aplicaciones biomédicas, en particular, es muy común que los sensores conviertan señales fisiológicas a un voltaje con una amplitud muy pequeña para que sea detectada con los circuitos convencionales. Por lo tanto, es importante ser capaz de escalar el voltaje por una constante (por ejemplo 100x).

El problema inverso -es decir, atenuar señales- es relativamente facil de resolver con un divisor de voltaje. Si deseamos, por ejemplo, dividir una señal de voltaje en 100, basta construir un divisor de voltaje con resistencias que obedecen la siguiente relación: $R_1 = 99 R_2$

$V_o = V_i / 100$

Pero, ¿cómo producir una señal que sea más grande que la entrada? ¿Qué tipo de circuito sería capaz de amplificar voltajes ?

Modelo de 2 compuertas

En ésta unidad nos concentraremos en entender qué características tienen circuitos amplificadores, y cómo utilizarlos, sin que sea necesario entrar en detalles de cómo se construyen. Partiremos imaginando que cualquier circuito amplificador necesita una entrada y una salida. Además, como todos los voltajes son relativos, agregaremos conexiones para el voltaje de referencia (la tierra):

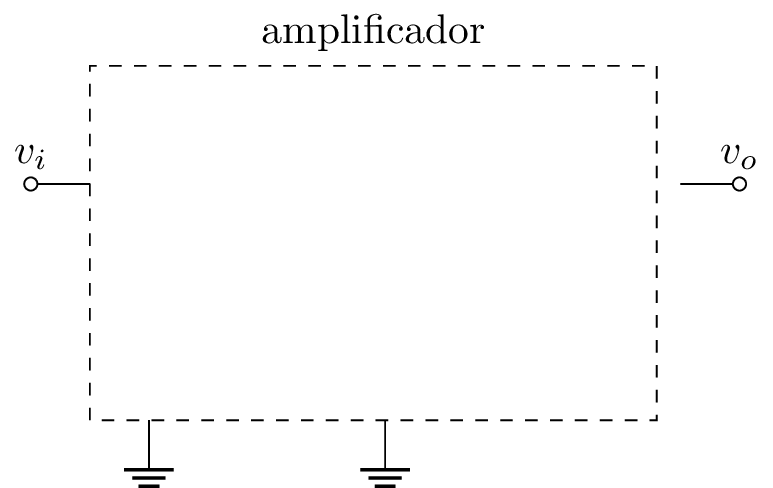
Este modelo se denomina modelo de 2 compuertas (1 de entrada y 1 de salida).

Aunque no sepamos los detalles de la implementación de un amplificador, es necesario tener un modelo eléctrico para poder resolver los circuitos que los incluyen. Para obtener el modelo, vamos a conectar un voltaje genérico a la entrada ($v_i$) y calcular el equivalente de Thevenin de la salida.

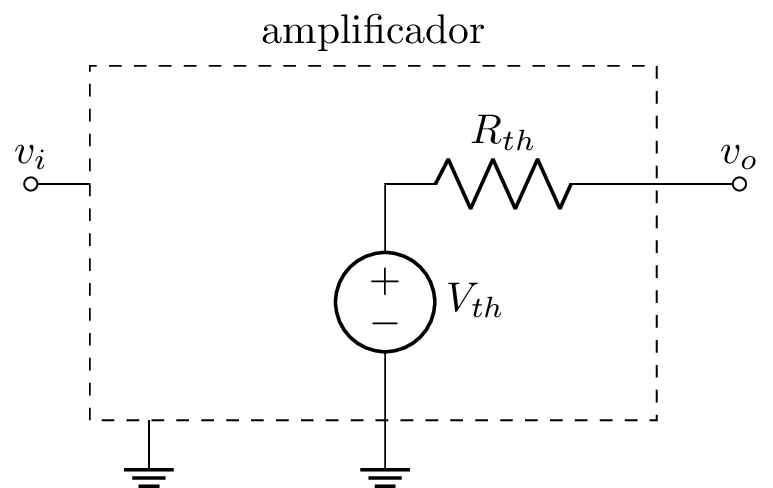
Para calcular $V_{th}$ simplemente medimos el voltaje en la salida $v_o$. La principal característica de un amplificador es que amplifica el voltaje, por lo que el voltaje $v_o$ medido será igual al voltaje de entrada $v_i$ multiplicado por una constante. Denominaremos la constante $A_V$ (factor de Amplificación de Voltaje), con lo cual obtenemos la siguiente relación:

$V_{th} = A_V * v_i$

No es posible determinar $R_{th}$ a priori, por lo que la dejaremos como un parametro del amplificador, y la denominaremos resistencia de salida, con el símbolo $R_o$ (output Resistance).

Para modelar la entrada del amplificador, nuevamente utilizamos un equivalente de Thevenin. Al desconectar $v_i$ y medir el voltaje en la entrada normalmente se obtiene 0V. Esto es esperado pues se trata de la entrada del circuito y por lo tanto no produce un voltaje. Una fuente de voltaje de 0V es equivalente a un cortocircuito, por lo que la omitiremos del modelo. Por otro lado, al medir la resistencia entre el terminal de entrada y tierra, obtendremos algún valor para $R_{th}$. Tampoco se puede determinar el valor a priori, por lo que agregaremos más un parámetro al amplificador con este valor, y lo denominaremos resistencia de entrada, con el símbolo $R_i$ (input Resistance)

El modelo finalizado se muestra a continuación

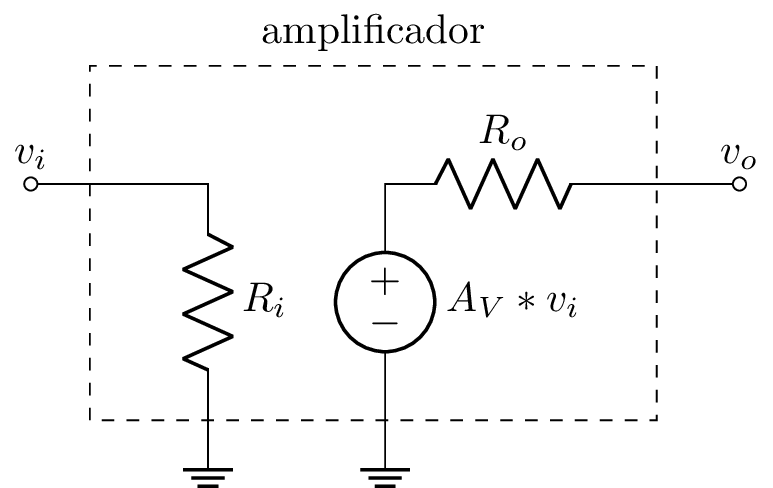
Ejemplo

Suponga que un determinado sensor produce una señal de voltaje $v_s = 0.001 cos(\omega t)$, con $\omega = 2000\pi$. Es decir, una señal sinusoidal con amplitud 1 mV. Dicha señal se conecta a un amplificador con $R_i = 50\ k\Omega$, $R_o=1\ k\Omega$ y $A_V = 20$. ¿Cual es la amplitud de la señal en la salida del amplificador ($v_o$) ? ¿En cuanto cambia la respuesta si $A_V = -20$ ?

Respuesta: 20 mV en ambos casos.

Efecto de $R_L$

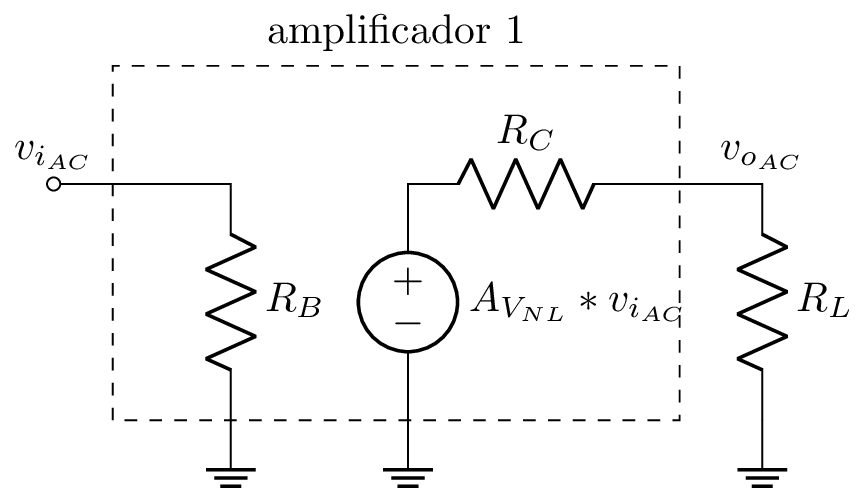
Así como modelamos la entrada del amplificador como una resistencia $R_i$, podemos igualmente modelar el resto del circuito que se conectará a la salida del amplificador como una resistencia de carga $R_L$ (Load Resistance). Es decir, de forma general el circuito que se conectará a la salida del amplificador se puede reemplazar por una resistencia $R_L$, conforme la figura a continuación:

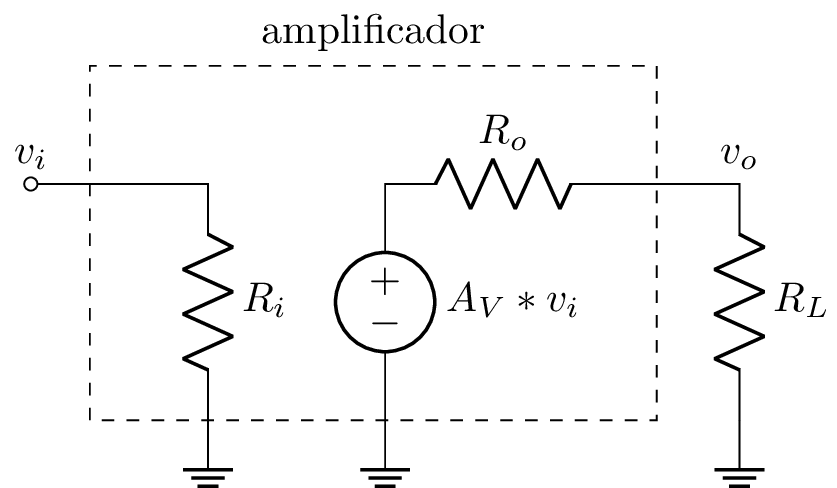
Se observa que el voltaje de salida del amplificador ya no es simplemente $A_V * v_i$, pues se forma un divisor de voltaje entre $R_o$ y $R_L$. Aplicando la forma de divisor de voltaje, se obtiene que el voltaje de salida del sistema completo es:

$v_o = \frac{R_L}{R_L+R_o} A_{V} v_i $

Para no confundir el $A_V$ del amplificador con el factor de amplificación del sistema completo (incluyendo la carga), llamaremos a la ganancia del amplificador sin carga $A_{V_{NL}}$ (NL = no load).

De ésta forma, la ganancia con carga $A_V$ se puede escribir como:

$\frac{v_o}{v_i} = A_V = \frac{R_L}{R_L+R_o} A_{V_{NL}} $

Se puede notar que la ganancia con la carga se ve dismiuida por un factor $\frac{R_L}{R_L+R_o}$, que es menor que 1 (el denominador es mayor que el numerador).

Efecto de $R_S$

Si ahora modelamos el circuito que antecede al amplificador utilizando su equivalente de Thevenin, obtenemos:

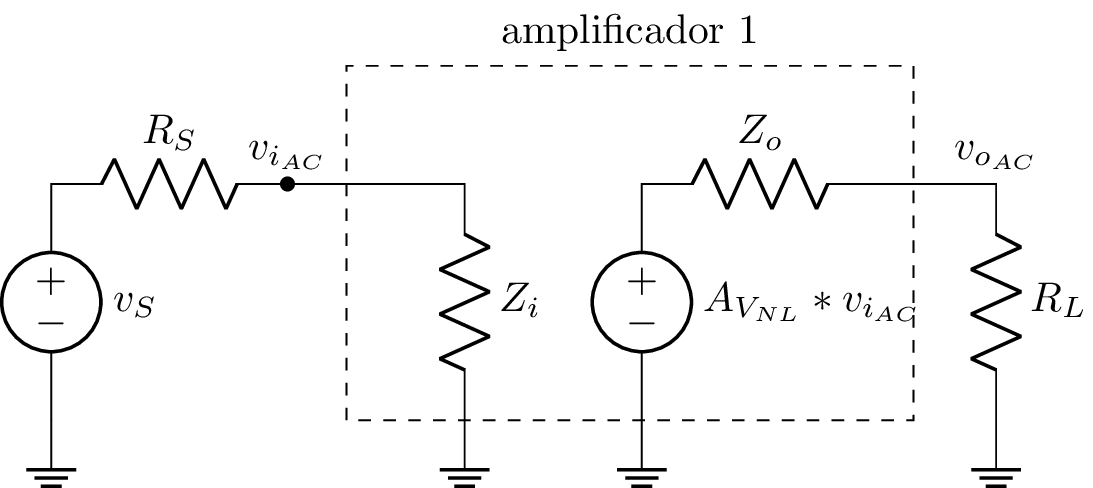
Donde $v_S$ es el voltaje del sensor y $R_S$ su resistencia de salida.

Utilizando el circuito completo, se puede mostrar que:

$v_{o} = \frac{R_i}{R_i+R_S} \frac{R_L}{R_L+R_o} A_{V_{NL}} v_S$

Es decir, la ganancia total es:

$A_{V} = \frac{v_{o}}{v_S} = \frac{R_i}{R_i+R_S} \frac{R_L}{R_L+R_o} A_{V_{NL}}$

Al igual que al agregar una carga, al considerar la resistencia de salida del circuito que antecede el amplificador la ganancia se ve reducida nuevamente, ésta vez por un factor $\frac{R_i}{R_i+R_S}$.

Un amplificador ideal y compromisos

Al diseñar un circuito amplificador, el objetivo es tener una alta ganancia de voltaje. Sin embargo, el efecto de las resistencias de entrada y de salida pueden afectar negativamente a la ganancia total. De ésta forma, al buscar minimizar el efecto de los factores asociados a dichas resistencias (hacerlos lo más cercanos a 1), es deseable que $R_i$ sea lo más grande posible y $R_o$ lo más pequeña posible. En el caso ideal,

En la práctica, no es posible mejorar todos los parámetros del amplificador, pues al mejorar uno puede que se afecte negativamente a otro. Más adelante veremos, por ejemplo, un circuito que tiene las siguientes fórmulas para $A_{V_{NL}}$ y $R_o$:

Podemos observar que si queremos disminuir $R_o$, es necesario disminuir $R_C$. Sin embargo, al hacerlo, también estamos disminuyendo la ganancia ($A_{V_{NL}}$). Hay compromisos similares con respecto a $R_i$. As veces es posible mejorar los 3 factores, pero aumentando el consumo de energía del amplificador, o el costo de sus componentes.

Bibliografia

Boylestad, R. & Nashelsky, L. (2009). Electrónica: Teoría de circuitos y dispositivos electrónicos (10ma.ed.)

Capítulos

Ejercícios Recomendados