SISTEMAS_ELECTRONICOS_PARA_INGENIERIA_BIOMEDICA
Respuesta en frecuencia II
Frecuencia de corte
La frecuencia de corte ($\omega_c$) es la frecuencia en que:
$A_V(\omega_c) = \frac{max(A_V(\omega))}{\sqrt{2}}$
En otras palabras, $A_V(\omega_c)$ es el $A_V(\omega)$ maximo dividido por $\sqrt{2}$
La origen del valor $\sqrt{2}$ es que se define la frecuencia de corte como la frecuencia en que la potencia de la señal es la mitad de la maxima. Como la potencia de una señal eléctrica es proporcional al voltaje al cuadrado, para reducir la potencia a la mitad basta reducir el voltaje por $\sqrt{2}$.
$pot \propto V^2 \implies pot = K V^2$
$\therefore \frac{pot}{2} = K(\frac{V}{\sqrt{2}})^2$
Recordatorio: para encontrar el maximo de una función se calcula el valor de la función cuando su derivada es cero y también en los extremos del intervalo. En el caso de $A_v(\omega)$, los extremos del intervalo son $\omega = 0$ y $\omega \to +\infty$
Ejemplo:
- Encuentre la frecuencia de corte del circuito estudiado en la clase anterior.
$H(s) = \frac{1}{RCs+1}$
$A_v(\omega) = |H(j\omega)| = |\frac{1}{RCj\omega+1}|$
$A_v(\omega) = \frac{1}{\sqrt{(RC\omega)^2+1}} = \frac{1}{\sqrt{R^2C^2\omega^2+1}}$
Se observa que $A_v(\omega)$ es una función estrictamente descendiente con respecto a $\omega$ (cuanto mayor $\omega$, menor $A_v(\omega)$). Por lo tanto, el valor maximo de $A_v(\omega)$ se da en el extremo inferior del intervalo ($\omega = 0$):
$max(A_V(\omega)) = A_V(0) =\frac{1}{\sqrt{R^2C^20^2+1}} = 1$
Por lo tanto, para encontrar la frecuencia de corte:
$A_V(\omega_c) = \frac{max(A_V(\omega))}{\sqrt{2}}$
$\frac{1}{\sqrt{R^2C^2\omega_c^2+1}} = \frac{1}{\sqrt{2}}$
$\frac{1}{R^2C^2\omega_c^2+1} = \frac{1}{2}$
$R^2C^2\omega_c^2+1 = 2$
$R^2C^2\omega_c^2 = 1$
$\omega_c^2 = \frac{1}{R^2C^2}$
$\omega_c = \frac{1}{RC}$
Nótese que la frecuencia de corte se obtiene en $rad/s$. Si se desea obtener el valor en Hz:
$f_c = \frac{\omega_c}{2\pi}$
$f_c = \frac{1}{2\pi RC}$
Filtros Activos
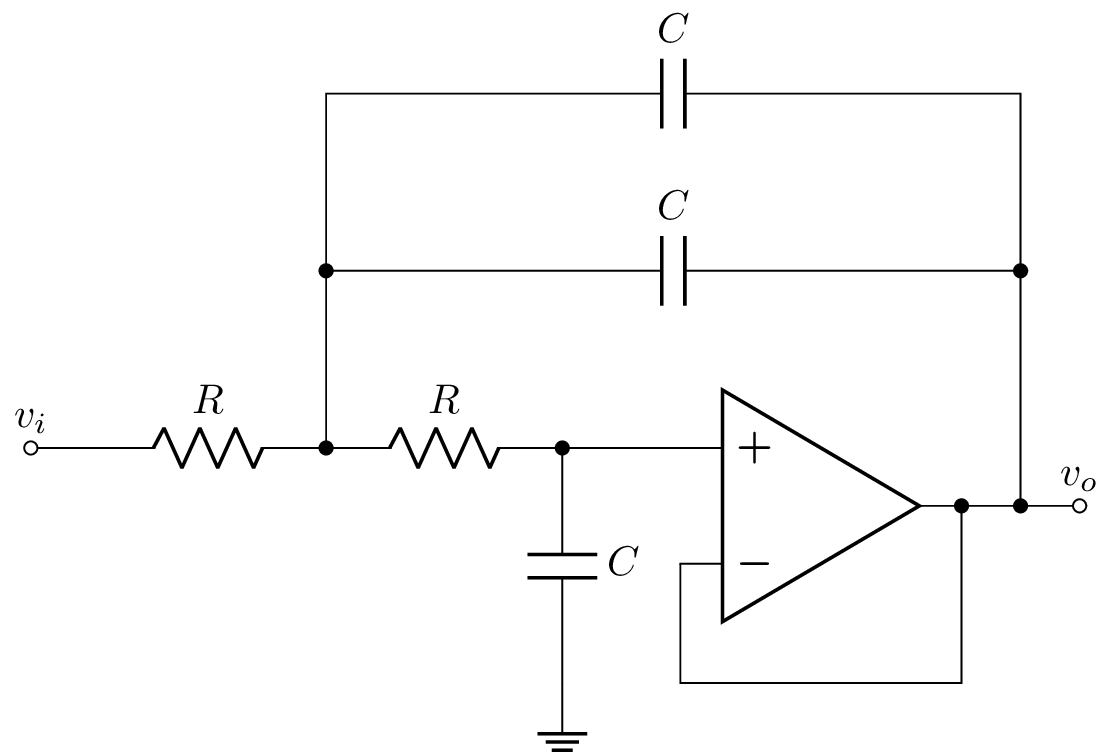
- Encuentre una fórmula para la frecuencia de corte del siguiente circuito:
Capítulos del libro
- Capítulo 9
- sesiones 9.4, 9.6 y 9.7
- Capítulo 11
- sesión 11.6
Ejercicios recomendados
- Capítulo 11
- ejercicios 15, 16 y 17